Electromagnetic Radiation and Atomic Spectrum
Electromagnetic Radiation and Atomic Spectrum
Electromagnetic radiations: The radiations which are associated with electrical and magnetic fields are called electromagnetic radiations. When an electrically charged particle moves under acceleration, alternating electrical and magnetic fields are produced and transmitted. These fields are transmitted in the form of waves. These waves are called electromagnetic waves or electromagnetic radiations.
Properties of electromagnetic radiations:
(i) Oscillating electric and magnetic field is produced by oscillating charged particles. These fields are perpendicular to each other and both are perpendicular to the direction of propagation of the wave.
(ii) They do not need a medium to travel. That means they can even travel in a vacuum.
Characteristics of electromagnetic radiations:
(i) Wavelength (λ): It may be defined as the distance between two neighbouring crests or troughs of the wave as shown. It is denoted by λ.
(ii) Frequency (ν): It may be defined as the number of waves that pass through a particular point in one second.
(iii) Velocity (v): It is defined as the distance travelled by a wave in one second. In a vacuum, all types of electromagnetic radiations travel with the same velocity. Its value is 3 × 108 m sec-1. It is denoted by v
(iv) Wavenumber: Wavenumber is defined as the number of wavelengths per unit length.
(v) Velocity = frequency × wavelength c = νλ
Electromagnetic spectrum: It is the arrangement of electromagnetic radiations in order of increasing wavelengths or decreasing frequencies.
Particle Nature of Electromagnetic Radiation:
Planck’s Quantum Theory:
(i) The radiant energy is emitted or absorbed not continuously but discontinuously in the form of small discrete packets of energy called ‘quantum’. In the case of light, the quantum of energy is called a ‘photon’.
(ii) The energy of each quantum is directly proportional to the frequency of the radiation, i.e. E α υ or E= hυ where h = Planck’s constant = 6.626 x 10-27 Js.
(iii) Energy is always emitted or absorbed as an integral multiple of this quantum.
E = nhυ Where n=1,2,3,4,…..
Some of the experimental phenomena like diffraction and interference can be explained by the wave nature of electromagnetic radiation. But some phenomena like black body radiation, photoelectric effect, a variation of heat capacity of solids with temperature, line spectra of atoms etc. could not be explained by the wave nature of electromagnetic radiation.
Black body radiation: An ideal body that emits and absorbs all frequencies of radiations is called a black body and the radiation emitted by such a body is called black body radiation. The frequency distribution of radiation emitted from a black body depends only on its temperature.
Photoelectric effect: The phenomenon of ejection of electrons from the surface of the metal (for example potassium, rubidium, caesium etc.) when the light of suitable frequency strikes it is called the photoelectric effect. 
The ejected electrons are called photoelectrons. Photoelectric work function (Wo): The minimum energy required to eject electrons is called the photoelectric work function.
Wo = hvo
Energy of the ejected electrons: hv = hvo + ½ mv2
Energy of the ejected electrons: h(v – vo) = ½ mv2
Where m is the mass of the electron and v is the velocity of the ejected electron. A more intense beam of light contains a larger number of photons, so the number of electrons ejected is also larger.
Dual Behaviour of Electromagnetic Radiation:
Electromagnetic radiations possess both particle and wave nature. This is known as the dual nature of Electromagnetic Radiation.
Electromagnetic Radiation and Atomic Spectrum:
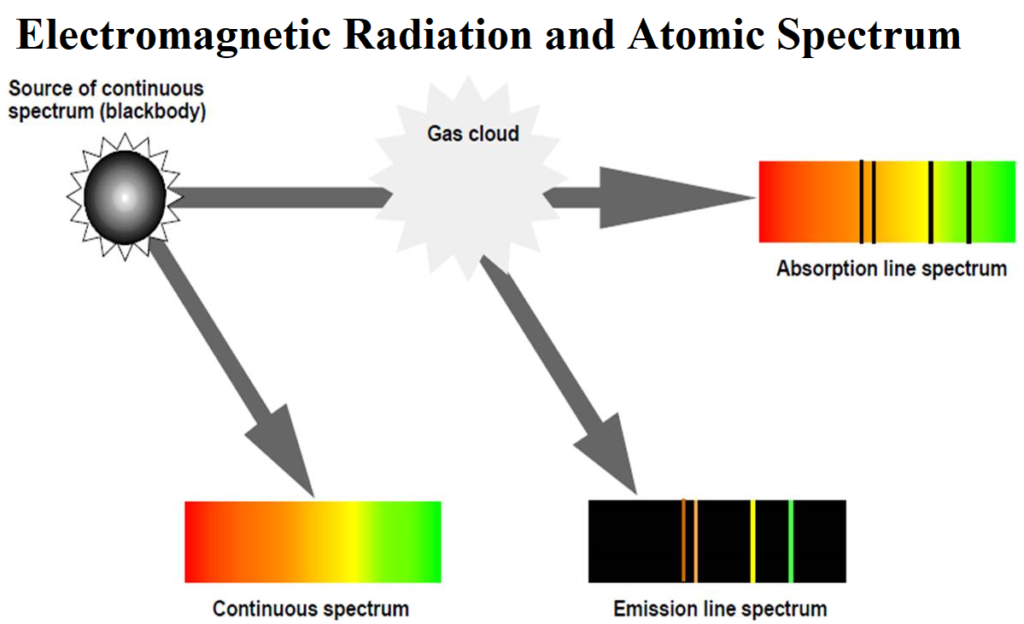
Atomic Spectra: When white light is passed through a prism, it splits into a series of coloured bands known as spectrum.
when electromagnetic radiation interacts with matter, atoms and molecules may absorb energy and reach a higher energy unstable state. To attain stability, they emit radiations in the form of a spectrum. Such a spectrum is called Atomic Spectrum.
Spectrum is of Two Types: Continuous and Line spectrum
(i) The spectrum which consists of all the wavelengths is called Continuous Spectrum.
(ii) A spectrum in which only specific wavelengths are present is known as a Line spectrum. It has bright lines with dark spaces between them. Line emission spectra are very useful in the study of the electronic structure of atoms. Each element has a unique line emission spectrum. The characteristic lines in atomic spectra can be used in chemical analysis to identify unknown atoms in the same way as finger-prints are used to identify people. So, line emission spectra are also called finger-print of atoms.
Emission and Absorption Spectra:
The spectrum of radiation emitted by a substance that has absorbed energy is called an emission spectrum. Atoms, molecules or ions that have absorbed radiation are said to be “excited”. To produce an emission spectrum, energy is supplied to a sample by heating it or irradiating it and the wavelength (or frequency) of the radiation emitted is recorded.
An absorption spectrum is like the photographic negative of an emission spectrum. Here a continuum of radiation (like white light) is passed through a sample which absorbs radiation of certain wavelengths. The missing wavelengths leave dark spaces in the bright continuous spectrum.
Line Spectrum of the Hydrogen atom:
When an electric discharge is passed through gaseous hydrogen, the H2 molecules dissociate and the energetically excited hydrogen atoms produced emit electromagnetic radiation of discrete frequencies. The hydrogen spectrum consists of several series of lines named after their discoverers. The first five series of lines are Lyman, Balmer, Paschen, Brackett and Pfund series. Among these lines, the Balmer series is the only series that we can be visible (since it lies in the visible region of emr). Johannes Rydberg proposed an equation for finding the wavenumber of the different lines in the Hydrogen spectrum.
The expression is:
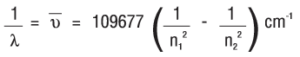
Where 109677 cm-1 is called the Rydberg constant.
Where n1 = 1, 2, 3,….. and n2 = n1 + 1, n1 + 2, ……
The different spectral lines, their n1 and n2 values and their spectral region are:
| Series | Spectral Region | n1 | n2 |
| Lyman | Ultraviolet | 1 | 2, 3, 4…. |
| Balmer | Visible | 2 | 3, 4, 5…. |
| Paschen | Infrared | 3 | 4, 5, 6…. |
| Bracket | Infrared | 4 | 5, 6, 7…. |
| Pfund | Infrared | 5 | 6, 7,8…. |
Electromagnetic Radiation and Atomic Spectrum
Thomsons and Rutherfords Atomic Model
The Discovery of Subatomic Particles
