Half-Life of Reactions in Chemical Kinetics
Half-Life of Reactions in Chemical Kinetics:
Pseudo First Order Reaction: The reactions which are not truly of first order but become reactions of first-order under certain conditions are called pseudo first-order reactions. For example,
- Hydrolysis of ester (H+).
CH3COOC2H5 + H2O → CH3COOH + C2H5OH
Rate = k [CH3COOC2H5] [H2O]
Since water is in excess and [H2O] is constant, so
Rate = k[CH3COOC2H5], Where k = k’[H2O]
- Inversion of cane sugar (in acid)
C12H22O11 + H2O → C6H12O6 + C6H12O6
Cane sugar Glucose Fructose
Since water is in excess and [H2O] is constant, so
Rate = k [C12H22O11]
Half-Life of a reaction (t1/2): It is the time in which the concentration of a reactant is reduced to one half of its initial concentration. It is represented by t1/2.
Half-Life of a Zero Order Reaction: For a zero-order reaction, the integrated rate law is:
k = [R0] – [R] t
When t = t1/2, [R] = ½ [R0]
On substituting these values in the above equation,
k = [R0] – ½ [R0] t1/2
t1/2 = [R0]/2k From the above relation, we can say the Half-Life of a zero-order reaction is directly proportional to the initial concentration of the reactants and inversely proportional to the rate constant.t1/2 = [R0]/2k
Half-Life of a First Order Reaction: For a first-order reaction, the integrated rate law is:

Rate of reaction and Temperature: Most of the chemical reactions are accelerated by an increase in temperature. It has been found that for a chemical reaction when the temperature is increased by 10°, the rate of the reaction and the rate constant is nearly doubled. The ratio of the rate constants of a reaction at two temperatures differing by 100 is called the temperature coefficient.
i.e., Temperature coefficient = Rate constant of the reaction at (T + 10)K Rate constant of the reaction at T K
The temperature dependence of the rate of a chemical reaction can be accurately explained by the Arrhenius equation. The equation is:
k = A e-Ea /RT ……………………………….. (1)
Where A is a constant called the Arrhenius parameter or the frequency factor or the pre-exponential factor. It is constant for a particular reaction. R is the universal gas constant and Ea is activation energy measured in joules/mole (J mol –1).
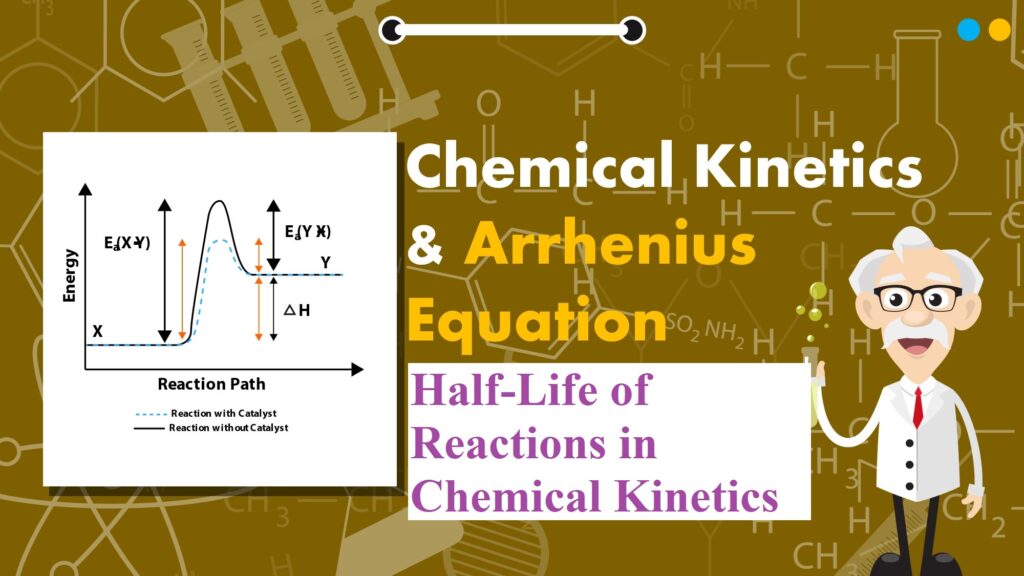
Threshold Energy: The minimum energy which the colliding molecules must have in order that the collision between them may be effective is called threshold energy.
Activation Energy: The minimum extra amount of energy absorbed by the reactant molecules so that their energy becomes equal to the threshold value is called activation energy.
Threshold energy = Activation energy + Energy possessed by the reactants
Less is the activation energy, faster is the reaction. In order that the reactants may change into products, they have to cross an energy barrier (corresponding to threshold energy). Reactant molecules absorb energy and form an intermediate called activated complex which immediately dissociates to form the products.
For Example:

Arrhenius equation: Quantitatively, the temperature dependence of the rate of a chemical reaction can be explained by Arrhenius equation
k = A e-Ea /RT
where A is the Arrhenius factor or the frequency factor or pre-exponential factor. R is gas constant and E a is activation energy measured in joules/mole.
The factor e – Ea /RT corresponds to the fraction of molecules that have kinetic energy greater than Ea.
Thus, it has been found from the Arrhenius equation that increasing the temperature or decreasing the activation energy will result in an increase in the rate of the reaction and an exponential increase in the rate constant.
Taking the natural logarithm of both sides of the equation
ln K = – Ea + ln A RT
At temperature T1, equation
ln K1 = – Ea + ln A RT1
At temperature T2, equation
ln K2 = – Ea + ln A RT2
(since A is constant for a given reaction)
K1 and K2 are the values of rate constants at temperatures T1 and T2 respectively.
Subtracting equation form, we obtain
ln K2 – ln K1 = Ea – Ea RT1 RT2

Effect of Catalyst: A catalyst is a substance which alters the rate of a reaction without itself undergoing any permanent chemical change. The action of the catalyst can be explained by intermediate complex theory. According to this theory, a catalyst participates in a chemical reaction by forming an intermediate complex. This is unstable and decomposes to yield products and the catalyst.

A catalyst increases the rate of a chemical reaction by providing an alternate pathway or reaction mechanism by reducing the activation energy between reactants and products. The important characteristics of a catalyst are:
- A small amount of the catalyst can catalyse a large number of reactants.
- A catalyst does not alter Gibbs energy, ΔG of a reaction. It catalyses the spontaneous reactions but does not catalyse non-spontaneous reactions.
- A catalyst does not change the equilibrium constant of a reaction, but it helps to attain the equilibrium faster by increasing the rate of both forward as well as backward reactions.
Collision Theory: This theory was developed by Max Trautz and William Lewis. It is based on the kinetic theory of gases. According to this theory, the reactant molecules are assumed to be hard spheres and reaction is occurred when molecules collide with each other. The number of collisions per second per unit volume of the reaction mixture is known as collision frequency (Z).
Another factor that affects the rate of chemical reactions is the activation energy.
For a bimolecular elementary reaction
A + B → Products
Rate of reaction can be expressed as
Rate (r)= ZAB e – Ea /RT
Where ZAB represents the collision frequency of reactants, A and B and e– Ea/RT represents the fraction of molecules with energies equal to or greater than Ea. Comparing with the Arrhenius equation, we can see that A is related to collision frequency.
A third factor that affects the rate of a chemical reaction is the proper orientation. To account for this, a factor P called the probability or steric factor is introduced. So the above equation becomes:
Rate (r)= PZAB e – Ea /RT
Half-Life of Reactions in Chemical Kinetics