Structure of Atom Notes Class 11
STRUCTURE OF ATOM
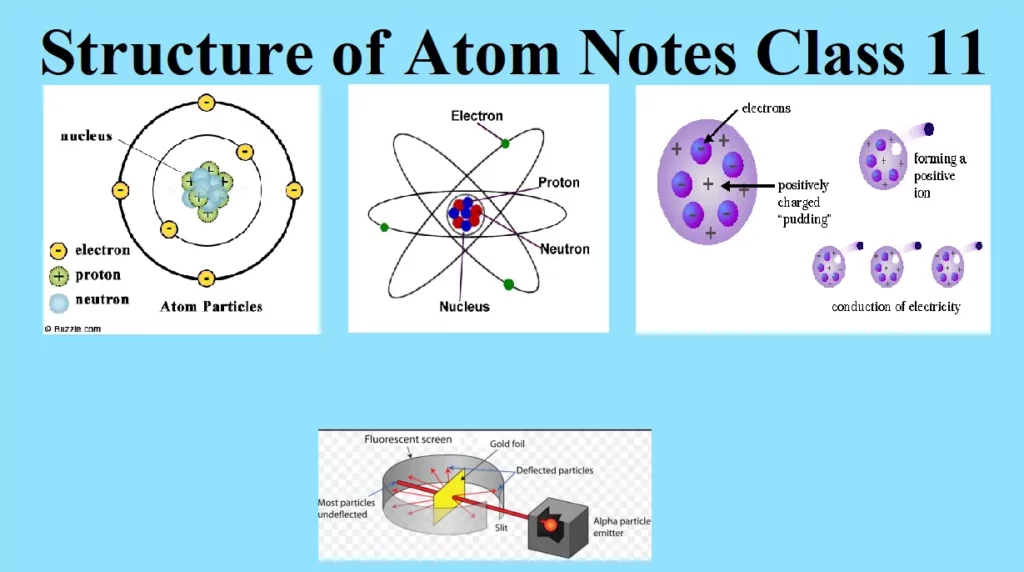
| Structure of Atom The term atom was introduced by Dalton and is defined as the smallest particle of an element that retains all its properties and identity during a chemical reaction. |
SUB – ATOMIC PARTICLE
(i) Discovery of Electron
Electron was discovered by J J Thomson by Cathode ray discharge tube experiment. A cathode-ray tube is made of glass containing two thin pieces of metal (called electrodes) sealed in it. The electrical discharge through the gases could be observed only at very low pressures and at very high voltages.

When a very high voltage (about 10,000 volts) is applied between the two electrodes, no electric discharge occurs at normal pressure. When the pressure of the gas inside the tube is less than 1 mm of mercury, a dark space appears near the cathode. When the pressure is reduced to 0.01 mm Hg, it fills the whole tube. When the pressure is further reduced (10-4 mm Hg), the electric discharge passes between the electrodes and the tube begins to glow. This is due to the striking of some invisible rays from the cathode. These rays which start from the cathode and move away from it, in straight lines are called cathode rays or cathode ray particles.
These rays can be further checked by making a hole in the anode and coating the tube behind anode with phosphorescent material like zinc sulphide. When these rays strike the zinc sulphide coating, a bright spot on the coating is developed.
Structure of Atom Notes Class 11
Properties of Cathode Rays
1. The cathode rays start from the cathode and move towards the anode.
2. They are invisible, but their behaviour can be observed with the help of fluorescent or phosphorescent materials.
3. In the absence of an electrical or magnetic field, these rays travel in straight lines.
4. In the presence of the electric or magnetic field, the cathode rays behave similarly to that of negatively charged particles. From this, it is clear that the cathode rays consist of negatively charged particles called electrons.
5. The characteristics of cathode rays (electrons) do not depend upon the material of electrodes and the nature of the gas present in the cathode rays.
6. These rays possess kinetic energy and hence can do mechanical work.
7. They can produce x-rays when incident on metals with high atomic mass.
Charge to Mass Ratio of Electron:
J.J. Thomson measured the ratio of electrical charge (e) to the mass of the electron (me) by using a cathode ray tube and applying electrical and magnetic field perpendicular to each other as well as to the path of electrons.

In the absence of an electric or magnetic field, the cathode rays hit the screen at point B. When only an electric field is applied, the electrons deviate from their path and hit the cathode ray tube at point A. Similarly, when only a magnetic field is applied, an electron strikes the cathode ray tube at point C. By carefully balancing the electrical and magnetic field strength, it is possible to bring back the electron beam to point B. From the strength of the electric and magnetic field, Thomson was able to calculate the value of e/me as:
e/me = 1.758 × 1011 C kg–1 Where me is the mass of the electron in kg and e is the magnitude of the charge on the electron in coulomb (C).
Charge on the Electron (e):
R.A. Millikan determined the charge on the electrons by a method known as the ‘oil drop experiment’. He found that the charge on the electron to be 1.6022 × 10–19 C.
Structure of Atom Notes Class 11
Mass of Electron (me):
The mass of the electron (me) was determined as follows:
Mass of electron (me) = e / e/me = 1.6022 x 10-19/1.758 x 1011
Mass of Electron = 9.1 × 10-31 kg
Discovery of Protons:
E. Goldstein modified the discharge tube experiment by perforated (with small holes) cathode. After evacuating the tube and on applying high voltage, he found that some rays were emitting behind the cathode and moving in the opposite direction of cathode rays. These rays deflect to the negative plate of the electric field. So they carry a positive charge and were called anode rays or canal rays.
Discovery of Neutrons:
Neutrons were discovered by James Chadwick by bombarding a thin sheet of beryllium by α-particles.
4Be9 + 2He4 → 6C12 + 0n1
They are electrically neutral particles having a mass slightly greater than that of the protons.
Characteristics of Sub – Atomic Particles:
| Sub Atomic Particle | Symbol | Discoverer | Absolute Charge (in Coulomb) |
Relative Charge | Mass In kg |
| Electron | e | J.J. Thomson | -1.6022 x 10-19 | -1 | 9.01×10-31 |
| Proton | p | E. Goldstein | +1.6022×10-19 | +1 | 1.6726×10-27 |
| Neutron | n | James Chadwick | 0 | 0 | 1.675×10-27 |
This is all about various experiments involved in The Discovery of Subatomic Particles.
Atomic Number: It is the number of protons present in the nucleus or the number of electrons present outside the nucleus.
It is denoted by the symbol ‘Z’.
Atomic number (Z) = nuclear charge or number of protons (p) = number of electrons (e)
Mass Number: It is the total number of protons and neutrons in atom. Or, it is the total number of nucleons in an atom. It is denoted by ‘A’.
i.e. Mass number (A) = no. of protons (p) + no. of neutrons (n) or, A = p + n
By knowing the atomic number and mass number, we can calculate the number of neutrons as:
n = A – Z If an element X has the atomic number Z and the mass number A, it is denoted as: ZXA
Types of Atomic Species
1. Isotopes: Atoms of the same element having the same atomic number but a different mass number. For example, isotopes of Hydrogen are 11H, 12H, 13H.
2. Isobars: Atoms of different elements having the same mass number but a different atomic number, e.g., 1840Ar, 1940K, 20Ca40
3. Isotones: Atoms of different elements which contain the same number of neutrons. e.g., 614C, 715N, 816
4. Isoelectronic Species: Atoms or ions containing the same number of electrons. For example, N3-, O2-, F–, Na+, Mg2+, Al3+, and Ne, having 10 electrons each are isoelectronic.
Structure of Atom Notes Class 11
ATOMIC MODELS:
Thomsons and Rutherfords Atomic Model
Thomsons and Rutherford’s Atomic Model is about the most important atomic models proposed during the study of the structure of atoms.
Thomson’s Model of Atom: J. Thomson proposed the first atomic model, which is known as the plum pudding or raisin pudding, or watermelon model. According to this model, an atom has a spherical shape in which the positive charge is uniformly distributed. The electrons are distributed in it, just like the seeds are distributed in a watermelon or plums are distributed in a pudding. An important feature of this model is that the mass of the atom is assumed to be uniformly distributed over the atom. Also, the total positive charge in an atom is equal to the total negative charge and hence the atom is electrically neutral.
Rutherford’s Nuclear Model of Atom:
Rutherford proposed an atomic model based on his α–particle scattering experiment. He bombarded a very thin gold foil (approximately 10-7m thickness) with α–particles.
Experiment: A stream of high-energy α–particles from a radioactive source was directed at a thin gold foil. The thin gold foil had a circular fluorescent zinc sulphide screen around it. Whenever α–particles struck the screen, a tiny flash of light was produced at that point.

Structure of Atom Notes Class 11
Observations: The important observations made by Rutherford are:
1. Most of the α– particles passed through the gold foil without any
2. A small fraction of the α–particles were deflected by small
3. A very few α– particles (∼1 in 20,000) bounced back, that is, were deflected by nearly 180°.
Conclusions: From the above observations, Rutherford made the following conclusions:
1. Since most of the α–particles passed through the foil without any deviation, most space in the atom is empty.
2. A few positively charged α– particles were deflected. This is because the positive charge of the atom is concentrated in a very small volume at the center called the nucleus.
3. The volume occupied by the nucleus is negligibly small as compared to the total volume of the atom. The radius of the atom is about 10–10 m, while that of the nucleus is 10–15
On the basis of the above observations and conclusions, Rutherford proposed the nuclear model (Planetary model) of an atom. According to this model:
1. All the positive charge and most of the mass of the atom is concentrated in an extremely small region called the nucleus.
2. Electrons are revolving around the nucleus with a very high speed in circular paths called an orbit.
3. Electrons and the nucleus are held together by electrostatic forces of attraction.
Drawbacks of Rutherford Model of an Atom:
Rutherford’s model cannot explain the stability of the atom.
According to Maxwell, electrons should emit electromagnetic radiations as an accelerated charged particle has the tendency of emitting electromagnetic radiation. Rutherford also stated that the electrons revolve around the nucleus in their orbits. Hence, due to the kinetic motion of the electrons, the energy of the moving electrons decreases continuously and ultimately electrons will fall inside the nucleus. Therefore, when Rutherford’s model was mixed with Maxwell’s theory, it was realized that the model is not appropriate.
Quantum Mechanics: Quantum mechanics takes into account the dual behavior of matter. An equation, given by Schrodinger, which has a better physical interpretation in terms of wave properties is Ĥ ψ = Eψ. Where Ĥ is called the Hamiltonian operator, E is the total energy of the system (K.E + P.E) and ψ is called the wave function.
Physical Significance of ψ: The wave function (ψ) is a mathematical function and it has no physical significance. Wave functions of hydrogen or hydrogen-like species with one electron are called atomic orbitals. All the information about the electron in an atom is stored in its orbital wave function ψ. Its square ψ2 is proportional to the probability of finding the electron at a given point around the nucleus and is always positive.He cannot explain the electronic structure of atom.
Electromagnetic Radiation and Atomic Spectrum
Electromagnetic radiations: The radiations which are associated with electrical and magnetic fields are called electromagnetic radiations. When an electrically charged particle moves under acceleration, alternating electrical and magnetic fields are produced and transmitted. These fields are transmitted in the form of waves. These waves are called electromagnetic waves or electromagnetic radiations.
Properties of electromagnetic radiations:
(i) Oscillating electric and magnetic field is produced by oscillating charged particles. These fields are perpendicular to each other and both are perpendicular to the direction of propagation of the wave.
(ii) They do not need a medium to travel. That means they can even travel in a vacuum.
Characteristics of electromagnetic radiations:
(i) Wavelength (λ): It may be defined as the distance between two neighbouring crests or troughs of the wave as shown. It is denoted by λ.
(ii) Frequency (ν): It may be defined as the number of waves that pass through a particular point in one second.
(iii) Velocity (v): It is defined as the distance traveled by a wave in one second. In a vacuum, all types of electromagnetic radiations travel with the same velocity. Its value is 3 × 108 m sec-1. It is denoted by v
(iv) Wavenumber: Wavenumber is defined as the number of wavelengths per unit length.
(v) Velocity = frequency × wavelength c = νλ
Electromagnetic spectrum: It is the arrangement of electromagnetic radiations in order of increasing wavelengths or decreasing frequencies.

Particle Nature of Electromagnetic Radiation:
Planck’s Quantum Theory:
(i) The radiant energy is emitted or absorbed not continuously but discontinuously in the form of small discrete packets of energy called ‘quantum’. In the case of light, the quantum of energy is called a ‘photon’.
(ii) The energy of each quantum is directly proportional to the frequency of the radiation, i.e. E α υ or E= hυ where h = Planck’s constant = 6.626 x 10-34 Js.
(iii) Energy is always emitted or absorbed as an integral multiple of this quantum.
E = nhυ Where n=1,2,3,4,…..
Some of the experimental phenomena like diffraction and interference can be explained by the wave nature of electromagnetic radiation. But some phenomena like black body radiation, photoelectric effect, a variation of heat capacity of solids with temperature, line spectra of atoms etc. could not be explained by the wave nature of electromagnetic radiation.
Black body radiation: An ideal body that emits and absorbs all frequencies of radiation is called a black body and the radiation emitted by such a body is called black body radiation. The frequency distribution of radiation emitted from a black body depends only on its temperature.

Photoelectric effect: The phenomenon of ejection of electrons from the surface of the metal (for example potassium, rubidium, caesium etc.) when the light of suitable frequency strikes it is called the photoelectric effect.  The ejected electrons are called photoelectrons. Photoelectric work function (Wo): The minimum energy required to eject electrons is called the photoelectric work function.
The ejected electrons are called photoelectrons. Photoelectric work function (Wo): The minimum energy required to eject electrons is called the photoelectric work function.
Wo = hvo
Energy of the ejected electrons: hv = hvo + ½ mv2
Energy of the ejected electrons: h(v – vo) = ½ mv2
Where m is the mass of the electron and v is the velocity of the ejected electron. A more intense beam of light contains a larger number of photons, so the number of electrons ejected is also larger.
Structure of Atom Notes Class 11
Dual Behaviour of Electromagnetic Radiation:
Electromagnetic radiations possess both particle and wave nature. This is known as the dual nature of Electromagnetic Radiation.
Electromagnetic Radiation and Atomic Spectrum:
Atomic Spectra: When white light is passed through a prism, it splits into a series of coloured bands known as spectrum.
when electromagnetic radiation interacts with matter, atoms and molecules may absorb energy and reach a higher energy unstable state. To attain stability, they emit radiations in the form of a spectrum. Such a spectrum is called Atomic Spectrum.
Spectrum is of Two Types: Continuous and Line spectrum
(i) The spectrum which consists of all the wavelengths is called Continuous Spectrum.
(ii) A spectrum in which only specific wavelengths are present is known as a Line spectrum. It has bright lines with dark spaces between them. Line emission spectra are very useful in the study of the electronic structure of atoms. Each element has a unique line emission spectrum. The characteristic lines in atomic spectra can be used in chemical analysis to identify unknown atoms in the same way as finger-prints are used to identify people. So, line emission spectra are also called finger-print of atoms.
Emission and Absorption Spectra:
The spectrum of radiation emitted by a substance that has absorbed energy is called an emission spectrum. Atoms, molecules or ions that have absorbed radiation are said to be “excited”. To produce an emission spectrum, energy is supplied to a sample by heating it or irradiating it and the wavelength (or frequency) of the radiation emitted is recorded.
An absorption spectrum is like the photographic negative of an emission spectrum. Here a continuum of radiation (like white light) is passed through a sample that absorbs radiation of certain wavelengths. The missing wavelengths leave dark spaces in the bright continuous spectrum.
Line Spectrum of the Hydrogen atom:
When an electric discharge is passed through gaseous hydrogen, the H2 molecules dissociate and the energetically excited hydrogen atoms produced emit electromagnetic radiation of discrete frequencies. The hydrogen spectrum consists of several series of lines named after their discoverers. The first five series of lines are Lyman, Balmer, Paschen, Brackett and Pfund series. Among these lines, the Balmer series is the only series that we can be visible (since it lies in the visible region of emr). Johannes Rydberg proposed an equation for finding the wavenumber of the different lines in the Hydrogen spectrum.
The expression is:
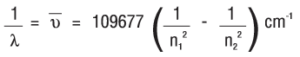
Where 109677 cm-1 is called the Rydberg constant.
Where n1 = 1, 2, 3,….. and n2 = n1 + 1, n1 + 2, ……
The different spectral lines, their n1 and n2 values and their spectral region are:
| Series | Spectral Region | n1 | n2 |
| Lyman | Ultraviolet | 1 | 2, 3, 4…. |
| Balmer | Visible | 2 | 3, 4, 5…. |
| Paschen | Infrared | 3 | 4, 5, 6…. |
| Bracket | Infrared | 4 | 5, 6, 7…. |
| Pfund | Infrared | 5 | 6, 7,8…. |
Structure of Atom Notes Class 11
Bohr’s Model & Heisenberg’s Uncertainty Principle
Bohr’s Model of Atom: The general features of the structure of the hydrogen atom and its spectrum was first explained by Niels Bohr. The important postulates of his theory are:
1. The electron in the hydrogen atom can move around the nucleus in circular paths of fixed radius and energy. These paths are called orbits or stationary states or allowed energy states. These energy levels are numbered as 1,2,3 etc or as K, L, M, N, etc. These numbers are known as Principal quantum numbers. 
2. The energy of an electron in an orbit does not change with time. However, when an electron absorbs energy, it will move away from the nucleus (i.e. to a higher energy level) and when it loses energy, it will move towards the nucleus (i.e. to a lower energy level). 
3. The radius of orbits can be given by the equation: rn = a0 n2 where a0 = 52.9
Thus, the radius of the first stationary state is 52.9 pm (called the Bohr radius). As n increases, the value of r will increase.
4. The energy of the electron in an orbit is given by the expression: En = -RH (1/n2), where n = 1,2,3…… and RH is a constant called Rydberg constant. Its value is 2.18×10-18. The energy of the lowest state (the ground state) is given by E1 = –2.18×10–18J. As the value of n increases, the energy of the electron also increases.
5. The frequency of radiation absorbed or emitted when the transition occurs between two stationary states that differ in energy by ΔE, is given by: ν = ΔE/h = E2 – E1/h
Where E1 and E2 are the energies of lower and higher energy levels respectively. This expression is commonly known as Bohr’s frequency rule.
6. The angular momentum of an electron is an integral multiple of h/2π. i.e. mevr = nh/2π
Where me is the mass of the electron, v is the velocity of electron and r is the radius of Bohr orbit. n = 1,2,3… Thus an electron can move only in those orbits whose angular momentum is an integral multiple of h/2π. So only certain fixed orbits are allowed.
Limitations of Bohr Atom Model: Bohr atom model could explain the stability and line spectra of the hydrogen atom and hydrogen-like ions (e.g. He+, Li2+, Be3+ etc). But it has the following limitations:
1. It could not explain the fine spectrum of the hydrogen atom.
2. It could not explain the spectrum of atoms other than the hydrogen atom.
3. It was unable to explain the splitting of spectral lines in the presence of the electric field (Stark effect) and in the magnetic field (Zeeman effect).
4. It could not explain the ability of atoms to form molecules by chemical bonds.
5. It did not consider the wave character of matter and Heisenberg’s uncertainty principle.
Dual Behaviour of Matter – de Broglie’s equation: The French physicist Louis de Broglie postulated that like radiation, matter also exhibits dual behaviour i.e., both particle and wave-like properties. The wavelength (l) of the matter-wave is related to the momentum (p) by the equation: λ = h/p = h/mv
Where m = mass, v = velocity and h is Planck’s constant.
The above equation is known as de Broglie’s equation
Heisenberg’s Uncertainty Principle: According to this law it is totally impossible to measure simultaneously, both the exact position and exact momentum (or velocity) of a moving microscopic particle or body.
Mathematically this law can be represented as:

Significance of Uncertainty Principle: Heisenberg’s Uncertainty Principle is significant only for the motion of microscopic objects and is not applicable to macroscopic objects. According to this Principle, we cannot determine the exact position and momentum of an electron. Thus, it rules out the existence of definite paths or orbits of electrons. We can only say the probability of finding an electron at a given point.
Structure of Atom Notes Class 11
Quantum Mechanics and Quantum Numbers
Quantum Mechanics and Quantum Numbers post provide complete information about quantum numbers with examples and wave function.
Quantum Mechanics: Quantum mechanics takes into account the dual behavior of matter. An equation, given by Schrodinger, which has a better physical interpretation in terms of wave properties is Ĥ ψ = Eψ. Where Ĥ is called Hamiltonian operator, E is the total energy of the system (K.E + P.E) and ψ is called the wave function.
Physical Significance of ψ: The wave function (ψ) is a mathematical function and it has no physical significance. Wave functions of hydrogen or hydrogen-like species with one electron are called atomic orbitals. All the information about the electron in an atom is stored in its orbital wave function ψ. Its square ψ2 is proportional to the probability of finding the electron at a given point around the nucleus and is always positive.
Quantum numbers: There are a set of four quantum numbers that specify the energy, size, shape, and orientation of an orbital. The Quantum number gives the address of the electron.
These are:
(i) Principal quantum number (n)
(ii) Azimuthal quantum number (l)
(iii) Magnetic quantum number (m)
(iv) Electron spin quantum number (ms)
Principal Quantum Number: The following formations are obtained from n.
1. It gives the size of the orbit.
2. It gives the energy of an electron in an orbit.
3. It gives the shell in which the electron is found.
4. It also gives the average distance between the electron and the nucleus. As the value of n increases, the distance between the electron and the nucleus also increases.
| n | 1 | 2 | 3 | 4 |
| Shell no. | K | L | M | N |
| Total number of orbitals in a shell = n2 | 1 | 4 | 9 | 16 |
| Maximum number of electrons = 2n2 | 2 | 8 | 18 | 32 |
Azimuthal quantum number (l): Azimuthal quantum number. ‘l’ is also known as orbital angular momentum or subsidiary quantum number. It identified the subshell and the three-dimensional shape of the orbital. It also determines the number of subshells or sub levels in a shell. The total number of subshells in a particular shell is equal to the value of n. l = 0, 1, 2… (n-1)
For example, when n = 1, the value of Ɩ is only 0.
For n = 2, the possible value of Ɩ can be 0 and 1.
For n = 3, the possible Ɩ values are 0,1 and 2.
Ɩ= 0 represents s orbital, Ɩ = 1 represents p orbital, Ɩ = 2 represents d orbital and Ɩ = 3 represents f orbital. The number of sub-shells in a principal shell is equal to the value of n.
When n = 1, Ɩ= 0. i.e. K shell contains only one sub-shell – s subshell
when n = 2, Ɩ = 0 and1. i.e. L shell contains two subshells – s and p subshells
when n = 3, Ɩ = 0, 1 and 2. i.e. M shell contains three subshells – s, p and d subshells.

Structure of Atom Notes Class 11
Magnetic Quantum Number (m): It gives information about the orientation of orbitals in space. For a given ‘Ɩ’ value, there are 2Ɩ+1 possible values for m and these values are given by: m = – Ɩ to 0 to + lThus for Ɩ = 0, m = 0 {2(0)+1 = 1}. i.e. s sub shell contains only one orbital called s orbital.
For Ɩ = 1, mƖ = –1, 0 and +1, {2(1)+1 = 3}. i.e. p subshell contains three orbitals called p orbitals (px, py and pz).
For Ɩ = 2, m = –2, –1, 0, +1 and +2, {2(2)+1 = 5}. i.e. d subshell contains five orbitals called d orbitals (dxy, dyz, dzx, dx2-y2, dz2).
Spin Quantum Number (s or ms): It refers to the orientation of the spin of the electron. It can have two values +1/2 and -1/2. +1/2 identifies the clockwise spin and -1/2 identifies the anti-clockwise spin.

Structure of Atom Notes Class 11
Summary of Quantum Numbers

Concept of Orbit and Orbital
 Structure of Atom Notes Class 11
Structure of Atom Notes Class 11
Shapes of Orbitals and Electronic Configuration
Shapes of Orbitals:
(i) s-orbitals: For s-orbitals, Ɩ = 0 and hence m = 0. So, there is only one possible orientation for s-orbitals. They are spherically symmetrical. The plots of probability density (ψ2) against distance from the nucleus (r) for 1s and 2s atomic orbitals are as follows:

For 1s orbital, the probability density is maximum at the nucleus and it decreases with an increase in r. But for 2s orbital, the probability density first decreases sharply to zero and again starts increasing. After reaching a small maximum it decreases again and approaches zero as the value of r increases. The region where the probability density (ψ2) reduces to zero is called nodal surface or node.
In general, for an ns-orbital, there are (n – 1) nodes.

All the s-orbitals are spherically symmetrical and their size increases with an increase in n.
s-orbital has a spherical shape

(ii) p-orbitals: For p-orbitals, Ɩ = 1 and mƖ = -1, 0, +1. i.e., there are three possible orientations for p orbitals. So, there are 3 types of p-orbitals – px, py, and pz. Each p orbital consists of two lobes. The probability density function is zero on the plane where the two lobes touch each other.
The size, shape, and energy of the three orbitals are identical. They differ only in the orientation of the lobes. For px orbital, the lobes are along the x-axis, for py, they are along the y-axis, and for pz, they are along the z-axis. All the p-orbitals have a dumb-bell shape.
Number of radial nodes = n – Ɩ – 1
Number of angular nodes = Ɩ
Total number of nodes = n-1
The diagrams for three 2p orbitals are as follows:

(iii) d-orbitals:
For d-orbitals, Ɩ = 2 and mƖ = -2, -1, 0, +1 and +2. i.e., there are five possible orientations for d orbitals. So there are 5 types of d-orbitals. They are dxy, dyz, dzx, dx2-y2, and dz2. The shapes of the first four d-orbitals are double dumb-bell and that of the fifth one, dz2, is dumb-bell having a circular collar in the xy-plane. The five d- orbitals have equivalent energies. For d-orbitals, the number of radial nodes is 2 and the total number of nodes is n-2. Boundary surface diagrams for d-orbitals are as follows:

(iv) f-orbitals:
For f-orbitals, Ɩ = 3 and mƖ = -3, -2, -1, 0, +1, +2 and +3. i.e., there are seven possible orientations for f orbitals. So there are 7 types of f-orbitals. They are fx3, fy3, fz3, fx(y2-z2), fy(z2-x2), fz(x2-y2) and fxyz. They have diffused shapes.
Electronic Configuration of Atoms: The arrangement of electrons in various orbitals is called the electronic configuration. This arrangement is obtained on the basis of following rules,
(i) Aufbau principle: Electrons are filled in the various orbitals in the increasing order of their energies, i.e., orbital having lowest energy will be filled first and the orbital having highest energy will be filled last.
 Structure of Atom Notes Class 11
Structure of Atom Notes Class 11
This rule has two sub rules:
a) The various orbitals are filled in the increasing order of their (n+Ɩ)
b) If two orbitals have the same (n+Ɩ) values, the orbital with the lower n value is filled first this rule is called Bohr-Bury rule. The increasing order of orbitals is asfollows:
1s < 2s < 2p < 3s <3p < 4s <3d < 4p <5s < 4d <5p < 6s < 4f < 5d < 6p < 7s

(ii) Pauli’s Exclusion Principle: No two electrons in an atom can have all the four quantum numbers the same. It can also be stated as – An orbital can have a maximum of two electrons and they must be of opposite spin.

(iii) Hund’s Rule of Maximum Multiplicity: No electron pairing takes place until each orbital is first singlifilled, e.g., N (7) has electronic configuration 1s2 2s2, 2px1 2py1 2pz1 according to Hund’s rule.

| Degenerate orbitals: Orbitals having the same energy are called degenerate orbitals. |
Shielding Effect or Screening Effect: Due to the presence of electrons in the inner shells, the electron in the outer shell will not experience the full positive charge on the nucleus. So due to the screening effect, the net positive charge experienced by the electron from the nucleus is lowered and is known as an effective nuclear charge.

Stability of Completely Filled and Half Filled Subshells:
(i) For atoms having half-filled or completely filled electronic configurations have extra stability compared to other atoms. This is due to their symmetrical distribution of electrons and greater exchange energy. For example, the electronic configuration of Cr is [Ar] 3d54s1 and not 3d44s2. This is because d5 represents a half-filled configuration and has extra stability. Similarly for Cu the electronic configuration is [Ar] 3d104s1 and not 3d94s2.

Another factor that explains the stability of half-filled orbitals is exchange energy. More the number of exchanges more is the stability.

Electronic Configuration of Elements From Hydrogen to Zinc:

Electronic Configuration Along with Orbital Diagram:

Structure of Atom Notes Class 11